La función plot
Pasamos ahora a plot, la función gráfica de caballo de batalla en el paquete base. El comando plot se presta naturalmente a gráficos bivariados. Para ver la suma total de argumentos que uno puede llamar usando plot, escriba args (plot.default) , que devuelve lo siguiente:
function (x, y=NULL, type="p", xlim=NULL, ylim=NULL,
log="", main=NULL, sub=NULL, xlab=NULL, ylab=NULL,
ann=par("ann"), axes=TRUE, frame.plot=axes,
panel.first=NULL, panel.last=NULL, asp=NA, ...)Obviamente, están sucediendo muchas cosas debajo de la función plot genérica . Con el fin de comenzar con la creación de figuras en R , queremos preguntarnos qué es esencial. La respuesta es sencilla: se debe especificar una variable x. Todo lo demás tiene un valor predeterminado o no es esencial. Para comenzar a experimentar con plot, continuamos utilizando los datos de cabildeo de salud del estado de 1997 cargados en la Sect. 3.1.1 .
Con plot, podemos trazar las variables por separado con el comando plot(varname), aunque esto es definitivamente menos informativo que los tipos de gráficos que se acaban de presentar en la Sección. 3.1 . Dicho esto, si simplemente quisiéramos ver todos los valores observados de la tasa de participación del lobby de las firmas financieras del estado de la salud (partratebusness), simplemente escribimos :
plot(health.fin$partratebusness,
ylab="Lobby Participation Rate")La figura 3.4 a se devuelve en la interfaz gráfica R. Tenga en cuenta que esta figura traza la tasa de participación del lobby contra el número de fila en el marco de datos: con datos transversales, este índice es esencialmente insignificante. Por el contrario, si estuviéramos estudiando datos de series de tiempo y los datos se clasificaran a tiempo, podríamos observar cómo evoluciona la serie a lo largo del tiempo. Tenga en cuenta que usamos la opción ylab porque, de lo contrario, el valor predeterminado etiquetará nuestro eje vertical con el aspecto de mal gusto health.fin$partratebusness. (Pruébelo y pregúntese qué pensaría el editor de una revista sobre cómo se ve el resultado).
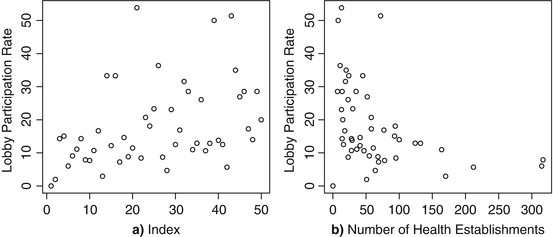
Figura 3.4 Tasa de participación del lobby de la industria de las finanzas de la salud solo y contra el número de establecimientos comerciales de finanzas de la salud. ( a ) Índice. ( b ) Número de establecimientos de salud
Por supuesto, estamos más interesados en las relaciones bivariadas. Podemos explorarlos fácilmente incorporando una variable x en el eje horizontal (generalmente una variable independiente) y una variable y en el eje vertical (generalmente una variable dependiente) en la llamada a graficar:
plot(y=health.fin$partratebusness,x=health.fin$supplybusiness,
ylab="Lobby Participation Rate",
xlab="Number of Health Establishments")Esto produce la figura 3.4 b, donde nuestro eje horizontal se define por el número de empresas de financiación de la salud en un estado, y el eje vertical se define por la tasa de participación del lobby de estas empresas en el estado respectivo. Este gráfico muestra lo que parece ser una disminución en la tasa de participación a medida que aumenta el número de empresas, quizás en una relación curvilínea.
Una herramienta útil es trazar la forma funcional de un modelo bivariado en el diagrama de dispersión de las dos variables. En el caso de la figura 3.4 b, es posible que deseemos comparar cómo una función lineal versus una función cuadrática o al cuadrado del número de empresas se ajusta al resultado de la tasa de participación del lobby. Para hacer esto, podemos ajustar dos modelos de regresión lineal, uno que incluye una función lineal de número de empresas y el otro que incluye una función cuadrática. Los detalles adicionales sobre los modelos de regresión se analizan más adelante en el Cap. 6 Nuestros dos modelos en este caso son:
finance.linear<-lm(partratebusness~supplybusiness,
data=health.fin)
summary(finance.linear)
finance.quadratic<-lm(partratebusness~supplybusiness+
I(supplybusiness^2),data=health.fin)
summary(finance.quadratic)El comando lm (linear model ) se ajusta a nuestros modelos y el comando summary resume nuestros resultados. Nuevamente, los detalles de lm se discutirán en el cap. 6 Con el modelo que es una función lineal del número de empresas, simplemente podemos ingresar el nombre de nuestro modelo ajustado (finance.linear) en el comando abline para agregar nuestra línea de regresión ajustada al gráfico:
plot(y=health.fin$partratebusness,x=health.fin$supplybusiness,
ylab="Lobby Participation Rate",
xlab="Number of Health Establishments")
abline(finance.linear)Como se mencionó anteriormente, el comando abline es particularmente flexible. Un usuario puede especificar a como la intersección de una línea y b como la pendiente. Un usuario puede especificar h como el valor del eje vertical donde se dibuja una línea horizontal, o v como el valor del eje horizontal donde se dibuja una línea vertical. O, en este caso, se puede insertar un modelo de regresión con un predictor para dibujar la línea de regresión que mejor se ajuste. Los resultados se presentan en la figura 3.5 a.
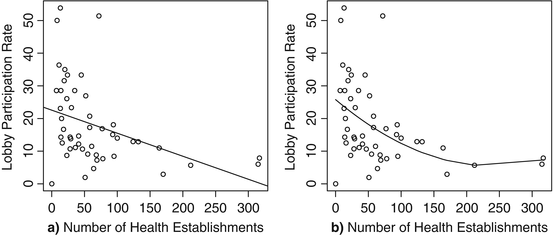
Figura 3.5 Tasa de participación del lobby de la industria financiera de la salud contra el número de establecimientos de salud, modelos lineales y cuadráticos. ( a ) Función lineal. ( b ) Función cuadrática
Alternativamente, podríamos volver a dibujar este gráfico con la relación cuadrática esbozada en él. Desafortunadamente, a pesar de la flexibilidad de abline, no puede trazar una relación cuadrática por defecto. La forma más fácil de trazar una forma funcional compleja es guardar los valores predichos del modelo, reordenar los datos según el predictor de interés y luego usar la función lines para agregar una línea conectada de todas las predicciones. Asegúrese de que los datos estén ordenados correctamente en el predictor; de lo contrario, la línea aparecerá como un desorden. El código en este caso es:
plot(y=health.fin$partratebusness,x=health.fin$supplybusiness,
ylab="Lobby Participation Rate",
xlab="Number of Health Establishments")
finance.quadratic<-lm(partratebusness~supplybusiness+
I(supplybusiness^2), data=health.fin)
health.fin$quad.fit<-finance.quadratic$fitted.values
health.fin<-health.fin[order(health.fin$supplybusiness),]
lines(y=health.fin$quad.fit,x=health.fin$supplybusiness)Este resultado se presenta en la figura 3.5 b. Si bien aún no entraremos en detalles de lm, observe que I(supplybusiness^2) se usa como predictor. I significa “como is,” por lo que nos permite calcular una fórmula matemática sobre la marcha. Después de volver a dibujar nuestro diagrama de dispersión original, estimamos nuestro modelo cuadrático y guardamos los valores ajustados en nuestro marco de datos como la variable quad.fit. En la cuarta línea, reordenamos nuestro marco de datos health.fin de acuerdo con los valores de nuestra variable de entrada supplybusiness. Esto se hace mediante el comando order, que enumera los índices vectoriales en orden de valor creciente. Finalmente, el comando lines toma nuestros valores predichos como las coordenadas verticales (y) y nuestros valores del número de empresas como las coordenadas horizontales (x). Esto agrega la línea al gráfico que muestra nuestra forma funcional cuadrática.
Gráficos lineales con plot
Hasta ahora, nuestros análisis se han basado en el plot predeterminado de dibujar un diagrama de dispersión. Sin embargo, en el análisis de series de tiempo, un gráfico de líneas a lo largo del tiempo suele ser útil para observar las propiedades de la serie y cómo cambia con el tiempo. (Más información sobre esto está disponible en el Capítulo 9 ) Volviendo a los datos sobre la cobertura de noticias televisivas de la política energética planteados por primera vez en la Sect. 3.1 , visualicemos el resultado de la cobertura de la política energética y un insumo del precio del petróleo.
Comenzando con la cantidad de historias de energía por mes, creamos esta trama de la siguiente manera:
plot(x=pres.energy$Energy,type="l",axes=F,
xlab="Month", ylab="Television Stories on Energy")
axis(1,at=c(1,37,73,109,145),labels=c("Jan. 1969",
"Jan. 1972","Jan. 1975","Jan. 1978","Jan. 1981"),
cex.axis=.7)
axis(2)
abline(h=0,col="gray60")
box()Esto produce la figura 3.6 a. En este caso, nuestros datos ya están ordenados por mes, por lo que si solo especificamos x sin y, R mostrará todos los valores en el orden temporal correcto8. ara designar que queremos un diagrama de líneas en lugar de un diagrama de dispersión de puntos, insertamos la letra l en la opción type = “l”. En este caso, hemos desactivado los ejes porque las marcas de graduación predeterminadas para el mes no son particularmente significativas. En su lugar, usamos el comando axis para insertar una etiqueta para el primer mes del año cada 3 años, ofreciendo una mejor sensación del tiempo real. Observe que en nuestra primera llamada a axis, usamos la opción cex.axis para encoger nuestras etiquetas al 70% del tamaño. Esto permite que las cinco etiquetas quepan en el gráfico. (Por ensayo y error, verá que R deja caer las etiquetas del eje que no encajarán en lugar de sobreimprimir el texto). Finalmente, usamos abline para mostrar el punto cero en el eje vertical, ya que este es un número significativo que refleja la ausencia completa. de la cobertura de la política energética en los informativos televisivos. Como demostraron nuestras cifras anteriores, vemos mucha más variabilidad y una media más alta después de los primeros 4 años. La cifra del precio del petróleo por barril se puede crear de manera similar:

Figura 3.6 Número de reportajes televisivos sobre política energética y precio del petróleo por barril, respectivamente, por mes. ( a
plot(x=pres.energy$oilc,type="l",axes=F,xlab="Month",
ylab="Cost of Oil")
axis(1,at=c(1,37,73,109,145),labels=c("Jan. 1969",
"Jan. 1972","Jan. 1975","Jan. 1978","Jan. 1981"),
cex.axis=.7)
axis(2)
box()Nuevamente, los datos están ordenados, por lo que solo se necesita una variable. La figura 3.6 b presenta este gráfico.
Construcción de figuras con plot: Detalles adicionales
Después de haber probado la mano con parcelas de la base de paquete, ahora itemize en detalle las funciones y opciones que aportan una considerable flexibilidad para crear figuras básicas en R . Tenga en cuenta que R en realidad ofrece la opción útil de comenzar con una pizarra en blanco y agregar elementos al gráfico bit a bit.
El sistema de coordenadas:
En la figura 3.4 , no nos preocupó establecer el sistema de coordenadas porque los datos efectivamente lo hicieron por nosotros. Pero a menudo, querrá establecer las dimensiones de la figura antes de trazar cualquier cosa, especialmente si está construyendo a partir del lienzo en blanco. El punto más importante aquí es que sus x e y deben ser de la misma longitud. Esto quizás sea obvio, pero los datos faltantes pueden crear dificultades que llevarán a R a oponerse.
Tipos de gráficos:
Ahora queremos graficar estas series, pero la función de trazado permite diferentes tipos de gráficos. Los diferentes tipos que se pueden incluir dentro de la función de gráfico genérico incluyen:
- type = “p” Esto es el valor predeterminado y grafica la x y y coordenadas como puntos.
- type = “l” Esto grafica la x y y coordenadas como líneas.
- type = “n” Esto grafica la x y y coordenadas como nada (solo configura el espacio de coordenadas).
- type = “O” Esto grafica la x y y coordenadas como puntos y líneas superpuestas (es decir, “overplots”).
- type = “h” Esto grafica la x y y coordenadas como un histograma como líneas verticales (también llamado diagrama de picos).
- type = “s” Esto grafica la x y y coordenadas como en pasos de escalera como líneas.
Ejes:
Es posible apagar los ejes, ajustar el espacio de coordenadas usando las opciones xlim e ylim, y crear sus propias etiquetas para los ejes.
- axes = Le permite controlar si los ejes aparecen en la figura o no. Si tiene fuertes preferencias sobre cómo se crean sus ejes, puede desactivarlos seleccionando axes = F dentro de plot y luego cree sus propias etiquetas usando el comando de axis separado : axis(side=1,at=c(2,4,6,8,10,12),labels=c(“Feb,” “Apr,”“June,”“Aug,”“Oct,”“Dec”))
- xlim =, ylim = Por ejemplo, si quisiéramos expandir el espacio desde el valor predeterminado de R , podríamos ingresar: plot(x=ind.var, y=dep.var, type=“o,” xlim=c(-5, 17),ylim=c(-5, 15))
- xlab = "“, ylab =”" Crea etiquetas para los ejes x e y.
Estilo:
Hay una serie de opciones para ajustar el estilo en la figura, incluidos cambios en el tipo de línea, grosor de línea, color, estilo de punto y más. Algunos comandos comunes incluyen:
- asp = Define el relación de aspecto de la gráfica. Establecer asp = 1 es una opción poderosa y útil que permite al usuario declarar que los dos ejes se miden en la misma escala. Consulte la Fig. 5.1 en la página 80 y la Fig. 8.4 en la página 159 como dos ejemplos de esta opción.
- lty = Selecciona el tipo de línea (sólida, discontinua, guión corto-largo, etc.).
- lwd = Selecciona el ancho de la línea (líneas gruesas o delgadas).
- pch = Selecciona el símbolo de trazado, puede ser un símbolo numerado (pch = 1) o una letra (pch = “D”).
- col = Selecciona el color de las líneas o puntos de la figura.
- cex = Factor de Character expansion (expansión de caracter) que ajusta el tamaño del texto y los símbolos en la figura. De manera similar, cex.axis ajusta el tamaño de la anotación del eje, cex.lab ajusta el tamaño de la fuente para las etiquetas del eje, cex.main ajusta el tamaño de la fuente del título y cex.sub ajusta el tamaño de la fuente de los subtítulos.
Parámetros gráficos:
La función par trae añadió funcionalidad para el trazado en R , dando el control del usuario sobre las representación gráfica (parameters). Una característica notable de par es que le permite trazar múltiples llamadas de plot en un solo gráfico. Esto se logra seleccionando par(new = T), mientras una ventana de trazado (o dispositivo) todavía está abierta y antes de la siguiente llamada a plot. Pero ten cuidado. Cada vez que use esta estrategia, incluya los comandos xlim e ylim en cada llamada para asegurarse de que el espacio de la gráfica se mantenga igual. También tenga cuidado de que los márgenes del gráfico no cambien de una llamada a la siguiente.
Funciones complementarias
También hay una serie de funciones complementarias que se pueden utilizar una vez que se ha creado el sistema de coordenadas básico mediante plot. Éstas incluyen: - arrows(x1, y1, x2, y2) Cree flechas dentro de la gráfica (útil para etiquetar puntos de datos particulares, series, etc.). - text(x1, x2, “text”) Cree texto dentro de la trama (modifique el tamaño del texto usando la opción de expansión de caracteres cex). - lineas (x, y) Crea una gráfica que conecte líneas. - puntos (x, y) Crea una gráfica de puntos. - polígono() Crea un polígono de cualquier forma (rectángulos, triángulos, etc.). - legend(x, y, at = c("“,”“), labels=c(”“,”")) Cree una leyenda para identificar los componentes de la figura. - axis(side) Agregue un eje con etiquetas predeterminadas o personalizadas a uno de los lados de un gráfico. Establezca el lado en 1 para la parte inferior, 2 para la izquierda, 3 para la parte superior y 4 para la derecha. - mtext(text, side) Comando para agregar margen de texto. Esto le permite agregar una etiqueta de eje a uno de los lados con más control sobre cómo se presenta la etiqueta. Consulte el código que produce la Fig. 7.1 en la página 114 para ver un ejemplo de esto.
Sin embargo, como alternativa, si un usuario tuviera algún índice de tiempo en el marco de datos, se podría producir un gráfico similar escribiendo algo como:
pres.energy\(Time<-1:180; plot(y=pres.energy\)Energy,x=pres.energy$Time,type=“l”).↩︎