Gráficos univariados en el paquete base
Como un primer vistazo a nuestros datos, mostrar una sola variable gráficamente puede transmitir un sentido de la distribución de los datos, incluyendo su modo, dispersión, sesgo y curtosis. La biblioteca de lattice en realidad ofrece algunos comandos más para la visualización univariante que la base, pero comenzamos con los principales comandos univariados incorporados. La mayoría de los comandos de gráficos en el paquete base llaman a la función plot, pero hist y boxplot son excepciones notables.
El comando hist es útil para simplemente tener una idea de la frecuencia relativa de varios valores comunes. Comenzamos cargando nuestros datos sobre la cobertura de noticias televisivas sobre política energética. Luego creamos un histograma de esta serie temporal de conteos mensuales de historias con el comando hist. Primero, descargue los datos de Peake y Eshbaugh-Soha sobre cobertura de pólizas de energía, el archivo llamado PESenergy.csv. El archivo está disponible en el Dataverse nombrado en la página vii o en el enlace de contenido del capítulo en la página 33. Es posible que deba usar setwd para apuntar R a la carpeta donde ha guardado los datos. Después de esto, ejecute el siguiente código:
pres.energy<-read.csv("PESenergy.csv")
hist(pres.energyEnergy,xlab="Television Stories",main="")
abline(h=0,col=’gray60’)
box()El resultado que produce este código se presenta en la figura 3.1 . En este código, comenzamos leyendo Peake y Eshbaugh-Soha (2008) datos. El archivo de datos en sí es un archivo de valores separados por comas con una fila de encabezado de nombres de variables, por lo que los valores predeterminados de read.csv se adaptan a nuestros propósitos. Una vez que se cargan los datos, trazamos un histograma de nuestra variable de interés usando el comando hist: pres.energy$Energy llama a la variable de interés desde su marco de datos. Usamos la opción xlab, que nos permite definir la etiqueta que imprime R en el eje horizontal. Dado que este eje nos muestra los valores de la variable, simplemente deseamos ver la frase “Historias de televisión,” describiendo brevemente lo que significan estos números. El opción main define un título impreso en la parte superior de la figura. En este caso, la única forma de imponer un título en blanco es incluir citas sin contenido entre ellas. Una característica interesante de graficar en el paquete base es que algunos comandos pueden agregar información adicional a una gráfica que ya se ha dibujado. El comando abline es una herramienta flexible y útil. (El nombre a-bline se refiere a la fórmula lineal \(y = a + bx\). Por lo tanto, este comando puede dibujar líneas con una pendiente y la intersección, o se puede dibujar una línea horizontal o vertical). En este caso, abline agrega un horizontal línea a lo largo del punto 0 en el eje vertical, por lo tanto \(h = 0\). Esto se agrega para aclarar dónde está la base de las barras en la figura. Finalmente, el comando box() encierra la figura completa en un cuadro, a menudo útil en artículos impresos para aclarar dónde termina el espacio gráfico y comienza el otro espacio en blanco. Como muestra el histograma, hay una fuerte concentración de observaciones en 0 y justo por encima de 0, y un claro sesgo positivo en la distribución. (De hecho, estos datos se vuelven a analizar en Fogarty y Monogan (2014) precisamente para abordar algunas de estas características de datos y discutir los medios útiles de analizar los recuentos de medios dependientes del tiempo).
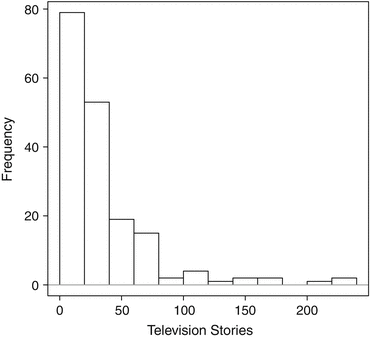
Figura 3.1 Histograma del recuento mensual de noticias de televisión relacionadas con la energía
Otro gráfico univariado es un diagrama de caja y bigotes. R nos permite obtener esto únicamente para la variable única, o para un subconjunto de la variable basado en alguna otra medida disponible. Primero dibujando esto para una sola variable:
boxplot(pres.energy$Energy,ylab="Television Stories")El resultado de esto se presenta en el panel (a) de la Fig. 3.2 . En este caso, los valores de los recuentos mensuales están en el eje vertical; por lo tanto, usamos la opción ylab para etiquetar el eje vertical (o el eje y label) apropiadamente. En la figura, la parte inferior del cuadro representa el valor del primer cuartil (percentil 25), la línea sólida grande dentro del cuadro representa el valor mediano (segundo cuartil, percentil 50) y la parte superior del cuadro representa el valor del tercer cuartil ( Percentil 75). Los bigotes, por defecto, se extienden a los valores más bajos y más altos de la variable que no son más de 1,5 veces el rango intercuartílico (o la diferencia entre el tercer y el primer cuartil) fuera de la caja. El propósito de los bigotes es transmitir el rango sobre el que cae la mayor parte de los datos. Los datos que quedan fuera de este rango se representan como puntos en sus valores respectivos. Esta gráfica de caja se ajusta a nuestra conclusión del histograma: los valores pequeños, incluido 0, son comunes y los datos tienen un sesgo positivo.
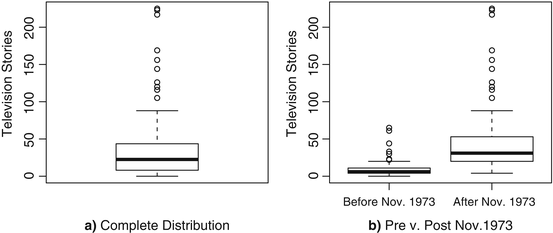
Figura 3.2 Tramas de caja y bigotes de la distribución del recuento mensual de nuevas historias televisivas relacionadas con la energía. El panel ( a ) muestra la distribución completa y el panel ( b ) muestra las distribuciones para los subconjuntos antes y después de noviembre de 1973
Los diagramas de caja y bigotes también pueden servir para ofrecer una idea de la distribución condicional de una variable. Para nuestra serie temporal de cobertura de la política energética, el primer evento importante que observamos es el discurso de Nixon de noviembre de 1973 sobre el tema. Por lo tanto, podríamos crear un indicador simple donde los primeros 58 meses de la serie (hasta octubre de 1973) se codifican con 0 y los 122 meses restantes de la serie (desde noviembre de 1973 en adelante) se codifican con 1. Una vez que hacemos esto, el comando boxplot nos permite condicionar sobre una variable:
pres.energy$post.nixon<-c(rep(0,58),rep(1,122))
boxplot(pres.energy$Energy~pres.energy$post.nixon,
axes=F,ylab="Television Stories")
axis(1,at=c(1,2),labels=c("Before Nov. 1973",
"After Nov. 1973"))
axis(2)
box()Esta salida se presenta en el panel (b) de la figura 3.2 . La primera línea de código define nuestra variable anterior a posterior a noviembre de 1973. Observe aquí que nuevamente definimos un vector con c. Dentro de c, usamos el comando rep (para repeat). Entonces rep(0,58) produce 58 ceros y rep(1,122) produce 122 unidades. La segunda línea dibuja nuestras gráficas de caja , pero agregamos dos advertencias importantes relativas a nuestra última llamada a la boxplot: Primero, enumeramos pres.energy\(Energy~pres.energy\)post.nixon como nuestro argumento de datos. El argumento antes de la tilde (~) es la variable para la que queremos la distribución, y el argumento posterior es la variable condicionante. En segundo lugar, agregamos el comando axes = F. (También podríamos escribir axes = FALSE, pero R acepta F como abreviatura). Esto nos da más control sobre cómo se presentan los ejes horizontal y vertical. En el comando siguiente, agregamos el eje 1 (el eje horizontal inferior), agregando etiquetas de texto en las marcas de verificación 1 y 2 para describir los valores de la variable condicionante. Luego, agregamos el eje 2 (el eje vertical izquierdo) y un cuadro alrededor de toda la figura. Panel (b) de la figura 3.2muestra que la distribución antes y después de esta fecha es fundamentalmente diferente. Los valores mucho más pequeños persisten antes del discurso de Nixon, mientras que hay una media más grande y una mayor dispersión de valores después. Por supuesto, esto es solo un primer vistazo y el efecto del discurso de Nixon se confunde con una variedad de factores, como el precio del petróleo, la aprobación presidencial y la tasa de desempleo, que contribuyen a esta diferencia.
Gráficos de barras
Los gráficos de barras pueden ser útiles siempre que queramos ilustrar el valor que toman algunas estadísticas para una variedad de grupos, así como para visualizar las proporciones relativas de datos medidos nominales u ordinalmente. Para ver un ejemplo de gráficos de barras, pasamos ahora al otro conjunto de datos de ejemplo de este capítulo, sobre el cabildeo por la salud en los 50 estados estadounidenses. Lowery y col. ofrecer un gráfico de barras de los promedios en todos los estados de la tasa de participación en el cabildeo, o el número de cabilderos como porcentaje del número de empresas, para todos los cabilderos de la salud y para siete subgrupos de cabilderos de la salud (2008, Fig. 3). Podemos recrear esa figura en R tomando las medias de estas ocho variables y luego aplicando la función de barplot al conjunto de medias. Primero debemos cargar los datos. Para hacer esto, descargue los datos de Lowery et al. Sobre cabildeo, el archivo llamado constructionData.dta . El archivo está disponible en el Dataverse nombrado en la página vii o en el enlace de contenido del capítulo en la página 33. De nuevo, es posible que deba usar setwd para apuntar R a la carpeta donde ha guardado los datos. Dado que estos datos están en formato Stata, debemos usar la biblioteca foreign y luego el comando read.dta:
library(foreign)
health.fin<-read.dta("constructionData.dta")Para crear la figura real en sí, podemos crear un subconjunto de nuestros datos que solo incluya los ocho predictores de interés y luego usar la función de apply para obtener la media de cada variable.
part.rates<-subset(health.fin,select=c(
partratetotalhealth,partratedpc,
partratepharmprod,partrateprofessionals,partrateadvo,
partratebusness,partrategov,rnmedschoolpartrate))
lobby.means<-apply(part.rates,2,mean)
names(lobby.means)<-c("Total Health Care",
"Direct Patient Care","Drugs/Health Products",
"Health Professionals","Health Advocacy","
Health Finance","Local Government","Health Education")En este caso, part.rates es nuestro marco de datos subconjunto que solo incluye las ocho tasas de interés de participación del lobby. En la última línea, el comando apply permite tener un marco de matriz o de datos (part.rates) y aplicar una función de interés (mean) a cualquiera de las filas o las columnas de la trama de datos. Queremos la media de cada variable y las columnas de nuestro conjunto de datos representan las variables. El 2, que es el segundo componente de este comando, le dice a apply que queremos aplicar la media a las columnas de nuestros datos. (Por el contrario, un argumento de 1 se aplicaría a las filas. Los cálculos basados en filas serían útiles si necesitáramos calcular alguna cantidad nueva para cada uno de los 50 estados.) Si simplemente escribimos lobby.means en la consola R ahora, imprimirá los ocho medios de interés para nosotros. Para configurar nuestra cifra de antemano, podemos adjuntar un nombre en inglés a cada cantidad que se informará en el margen de nuestra cifra. Hacemos esto con el comando de names y luego asignamos un vector con un nombre para cada cantidad.
Para dibujar realmente nuestro gráfico de barras, usamos el siguiente código:
par(mar=c(5.1, 10 ,4.1 ,2.1))
barplot(lobby.means,xlab="Percent Lobby Registration",
xlim=c(0,26),horiz=T,cex.names=.8,las=1)
text(x=lobby.means,y=c(.75,1.75,3,4.25,5.5,6.75,8,9),
labels=paste(round(lobby.means,2)),pos=4)
box()Los resultados se representan en la figura 3.3 . La primera línea llama al comando par, que permite al usuario cambiar una amplia gama de valores predeterminados en el espacio gráfico. En nuestro caso, necesitamos un margen izquierdo más grande, por lo que usamos la opción mar para cambiar esto, estableciendo el segundo valor en el valor relativamente grande de 10. (En general, los márgenes se enumeran como inferior, izquierdo, superior y luego derecho .) Todo lo que se ajuste con par se restablece a los valores predeterminados después de cerrar la ventana de trazado (o dispositivo, si se escribe directamente en un archivo). A continuación, usamos el comando barplot. El argumento principal es lobby.means, que es el vector de medias variables. El valor predeterminado de barplot consiste en dibujar un gráfico con líneas verticales. En este caso, sin embargo, configuramos la opción horiz = T para obtener barras horizontales. También usamos las opciones cex.names (character expansion for axis names o expansión de las caraterísticas en los nombres de los ejes) y las = 1 (label axis style) para reducir nuestras etiquetas de barras para el 80% de su tamaño por defecto y los obligan a imprimir en horizontal, respectivamente7. El comando xlab nos permite describir la variable para la cual estamos mostrando las medias, y el comando xlim (x-axis limits) nos permite establecer el espacio de nuestro eje horizontal. Finalmente, usamos el comando text para imprimir la media de cada tasa de registro de lobby al final de la barra. El comando text es útil cada vez que deseamos agregar texto a un gráfico, ya sean valores numéricos o etiquetas de texto. Este comando toma coordenadas x para su posición a lo largo del eje horizontal, y coordenadas para su posición a lo largo del eje vertical y labels valores para que el texto se imprima en cada punto. La opción pos = 4 especifica imprimir el texto a la derecha del punto dado (alternativamente 1, 2 y 3 especificarían abajo, izquierda y arriba, respectivamente), para que nuestro texto no se superponga con la barra.
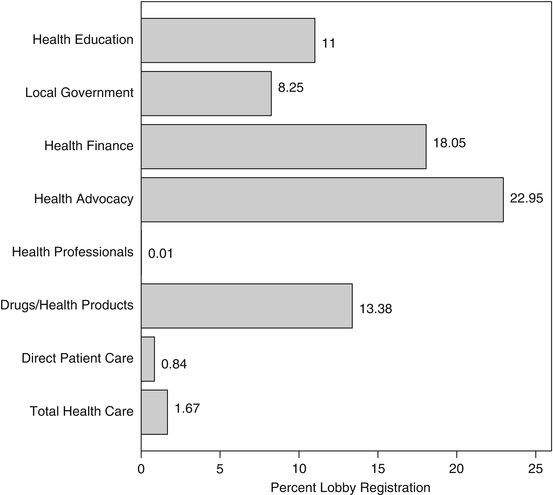
Figura 3.3 Gráfico de barras de la tasa media de participación de los grupos de presión en la atención médica y en siete subgremios en los 50 estados de EE.
El valor predeterminado de las es 0, que imprime etiquetas paralelas al eje. 1, nuestra elección aquí, los imprime horizontalmente. 2 imprime perpendicularmente al eje y 3 imprime verticalmente.↩︎